Brainfuck Compiler
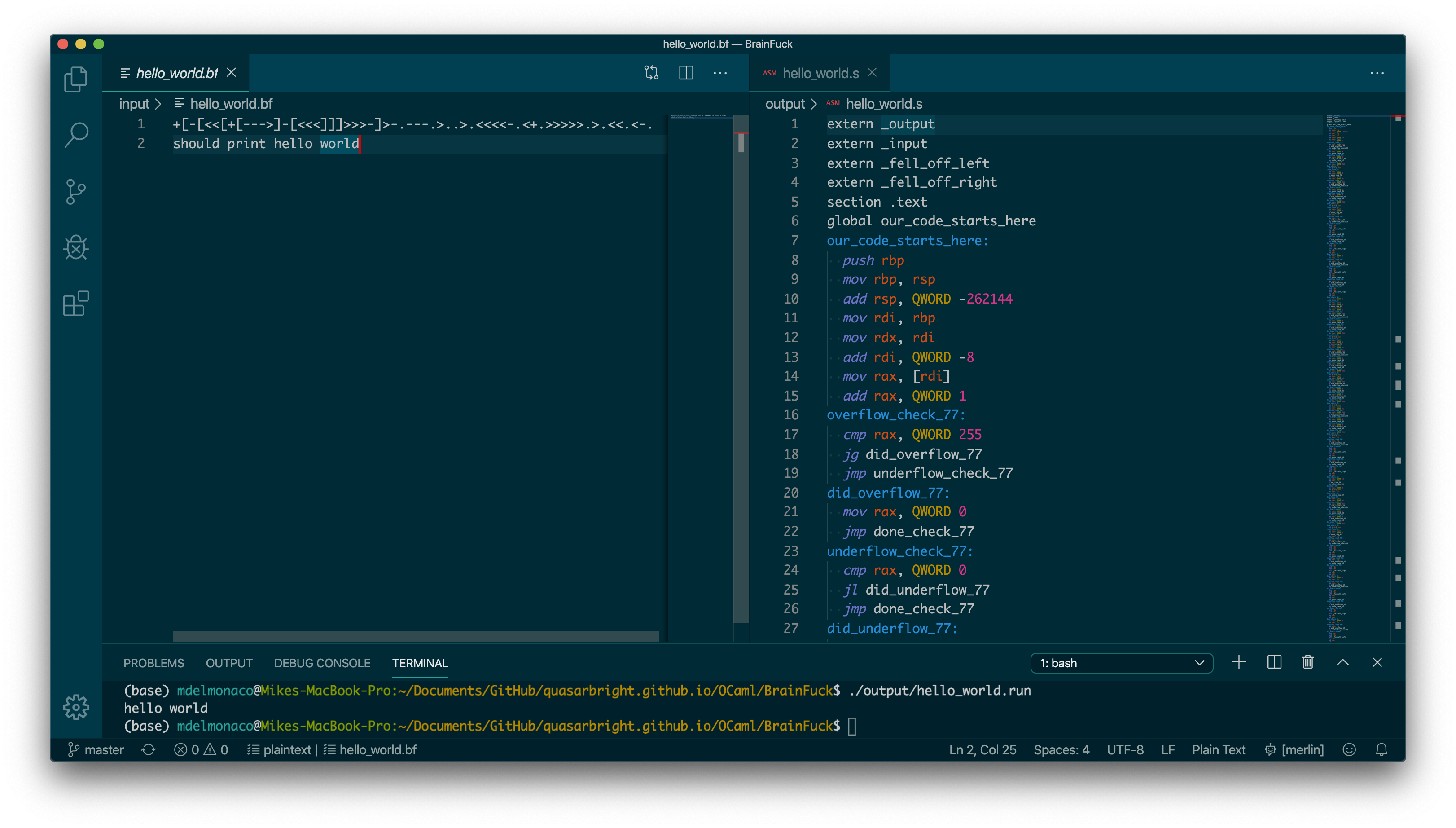
I made a compiler from Brainfuck to x86_64 assembly. I wanted to make a Turing-complete compiler, but I didn’t know how to make a good compiler for a fancy, high-level language yet. I also wanted to make something funny and ridiculous. It was tough to debug some problems I had with stack alignment and memory initialization, but it was really fun making the compiler and getting everything working.
The Brainfuck runtime is a long tape with cells containing integers in the range [0,255]. There is a read-write head which can move around the tape and increment and decrement cells. You can also print out the ASCII character corresponding to the integer in the cell under the head and read a character from user input, storing its ASCII value in the cell under the head. I treat the program’s stack in memory as the tape and restrict each value in memory to the range [0,255]. I keep track of the location of the head in the RDI register by storing the memory address of the head. I increment/decrement the value that is at the location in memory specified by the head. I allocate a little over 30,000 cells for the tape, shift RSP down by that amount, and use RBP and RSP as the bounds of the tape.
Regular Expression Matcher
I made a regular expression matcher. The regular expressions supported are pretty basic without much syntactic sugar, but are sufficient to describe all regular languages. I convert the regular expression into a non-deterministic finite automaton, optimize the it, then run run a list of symbols through it and see if it ends up in a success state. The coolest part is that I made everything type generic, so this could actually match regular expressions of any type, not just text characters. You could make a regular expression of integers, lists, or whatever you want. As long as you can define comparison for it, you can make regular expressions of it.
This was my first hobby project in OCaml. I discovered OCaml in a compilers course I’m taking and I loved it instantly. You can define and work with union types so easily and pattern matching is fantastic. I made a regular expression matcher in Java before this and it was a mess. It took me over a month and I had multiple failed attempts that I had to completely abandon. When I finally got it working, my I had around 20 files, many of them over 100 lines. When I made it in OCaml, it took me a few days and I only needed 3 files, none of them over 200 lines, and I had just learned the language. I think I’m going to use OCaml for most of my pure programming projects going forward. I might even remake Subduce in it because of how nice algebraic types and pattern matching are.
Regular Expression Minimum Satisfier Iterator
The sequel to my regular expression matcher. Given a regular expression, it iterates over all possible strings that satisfy the regular expression. And it does it in shortlex order! I also made this type generic like the regular expression matcher, so you can generate satisfiers of regular expressions of any symbol type.
Here’s the algorithm: Start out by converting the regular expression into a non-deterministic finite state automaton. Then, collapse the empty transitions such that every transition consumes a symbol. This can be done by following the empty transitions from a state until you hit a symbol transition, and collapsing that into one symbol transition. Then, do a breadth-first-search from the initial state, keeping track of the lists of symbols you’ve consumed in each state and recording the satisfying list of symbols when you hit an accepting state. If you keep the search going beyond when you hit the first transition, you’ll iterate over all satisfiers in order of ascending length. If you also want to go in lexicographic order, when you select the next state to push onto the queue, use the transition with the lexicographically lowest symbol.
To keep track of the list of symbols for each state, I did BFS with a queue of (state, symbol list) pairs. When I push another state on and consume a character, I add it to the list so it accumulates the word. Note that it’s possible to have the same state in the queue twice with different symbol lists.
The first thing I used it on was the regular expression for a natural number. When I ran it, it listed the natural number numbers in ascending order. That might be the most complicated way to count that I’ve ever seen. If you ever want a really contrived, ridiculous counted for-loop, there you go.
OCaml is a functional language and I like to try to keep things pure and immutable. Initially, I used a while loop that infinitely printed out satisfiers in order. But I wanted to make something like a java-like iterator or a python-like generator. Iterators and generators have an internal state that gets mutated when you get the next value. Since this is all a breadth-first-search, the “internal state” can be thought of as the queue of the search. And getting the next value is progressing the search until you hit the next accept state. Ok, so the state is the queue, the values are symbol lists that satisfy the regular expression, and the “get next” is continuing the search where you left off until you hit the next accepting state. Now how do you make an iterator that is immutable? I defined an iterator type that has a current state and a function that takes in a state and returns a pair containing the next value and the next state. Just for fun, I also defined abstractions like foldl, foldr, map, etc. Foldr only works on terminating iterators, but since foldl accumulates from the beginning of the iterator, I let the user provide a “break” predicate that can examine the current accumulated value and potentially terminate the fold. That way, you can foldl on an infinite iterator. I ended up making a pure iterator version of the whole thing and using foldl to loop waiting for user input to print the next satisfier. After all that, I realized OCaml has the seq type, which might be a better version of what I made.